パズルに挑戦
四角に切れ
【問題】
☆のマスを含む、二つの四角形の面積の合計はいくつでしょう?
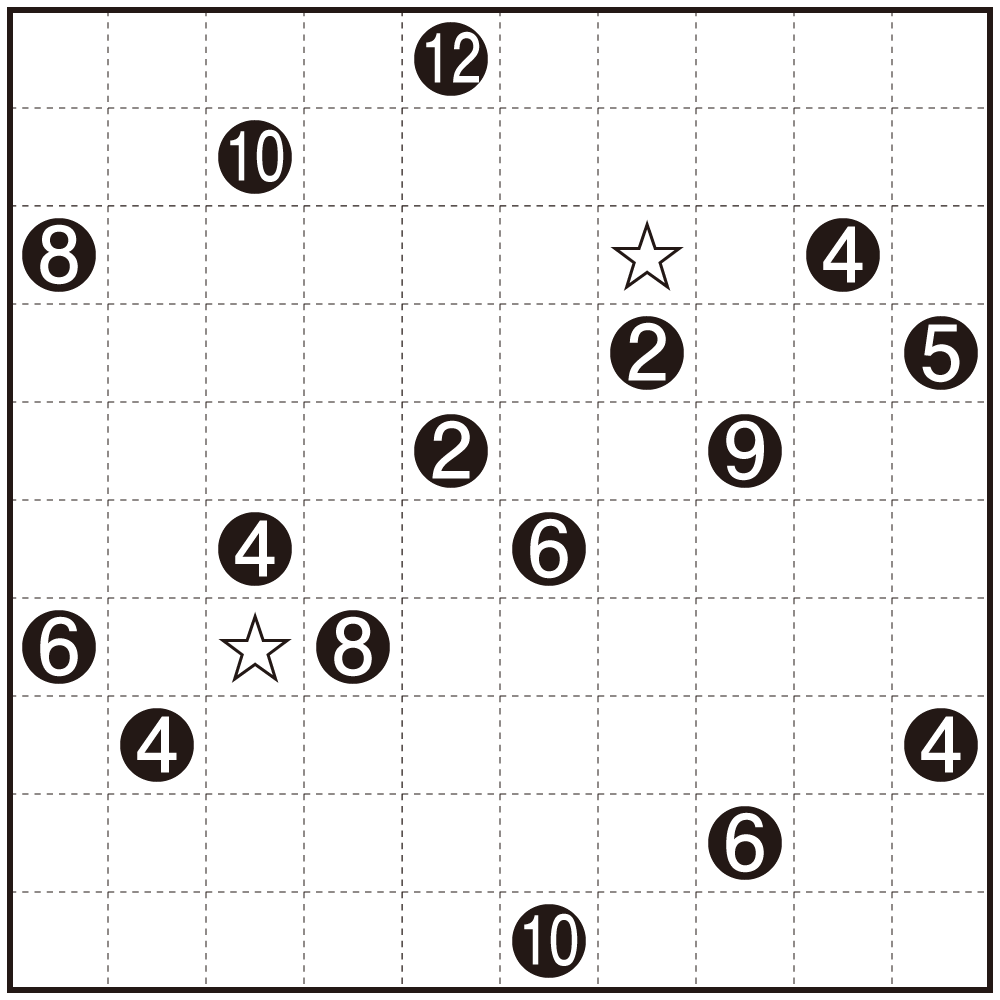
【ルール】
- ①点線の上にタテヨコに線を引き、盤面をいくつかの長方形(正方形も含みます)に分けましょう。
- ②どの長方形にも数字が1つずつ入るようにします。
- ③数字は、1マスの面積を1としたときに、その数字が入る長方形の面積がいくつになるかを表しています。たとえば「4」と書いてあるマスを含む長方形は、1×4、2×2、4×1のいずれかになります。
【考え方】
数字をヒントにして、盤面を四角形に切っていくパズルです。
例題で解き方を確認しましょう。

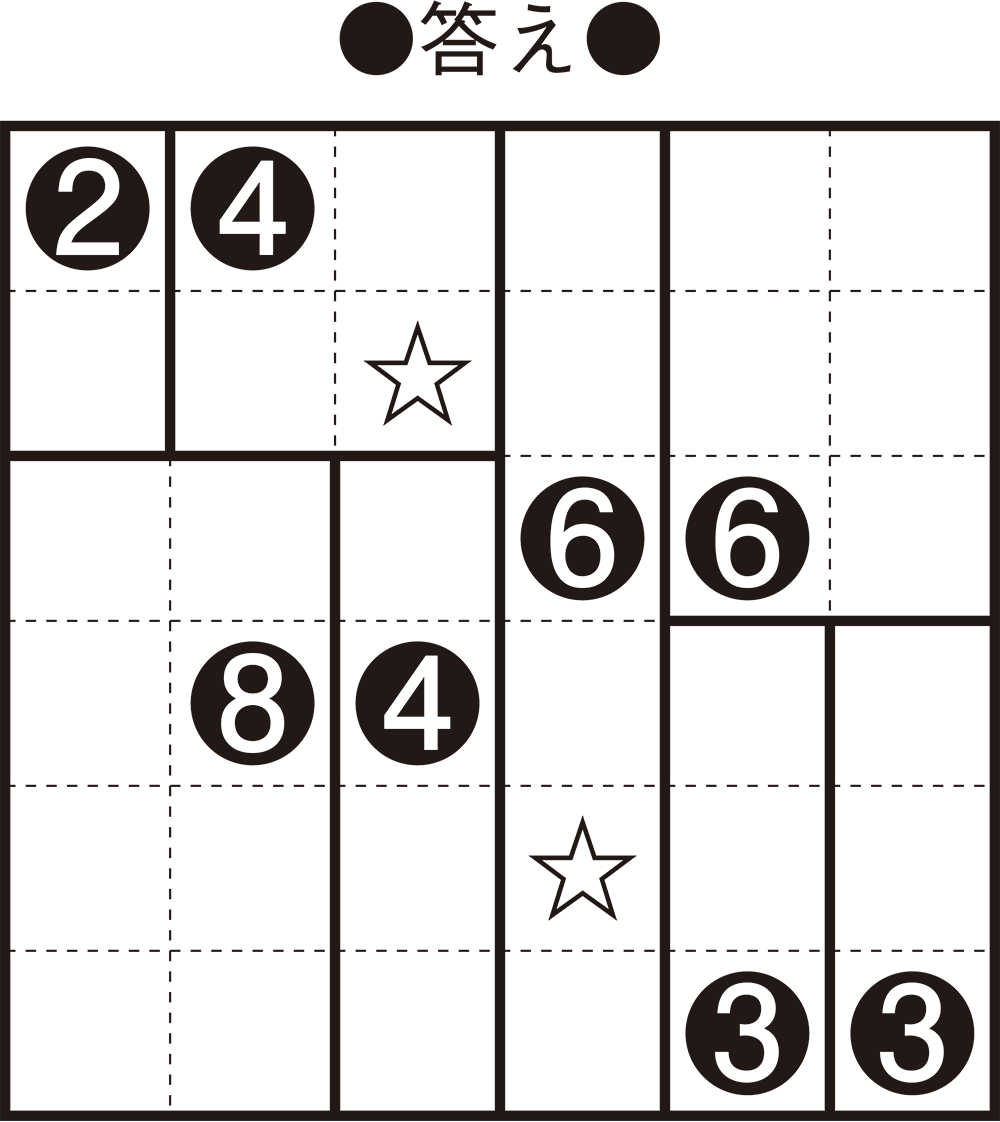
4+6=10でした。
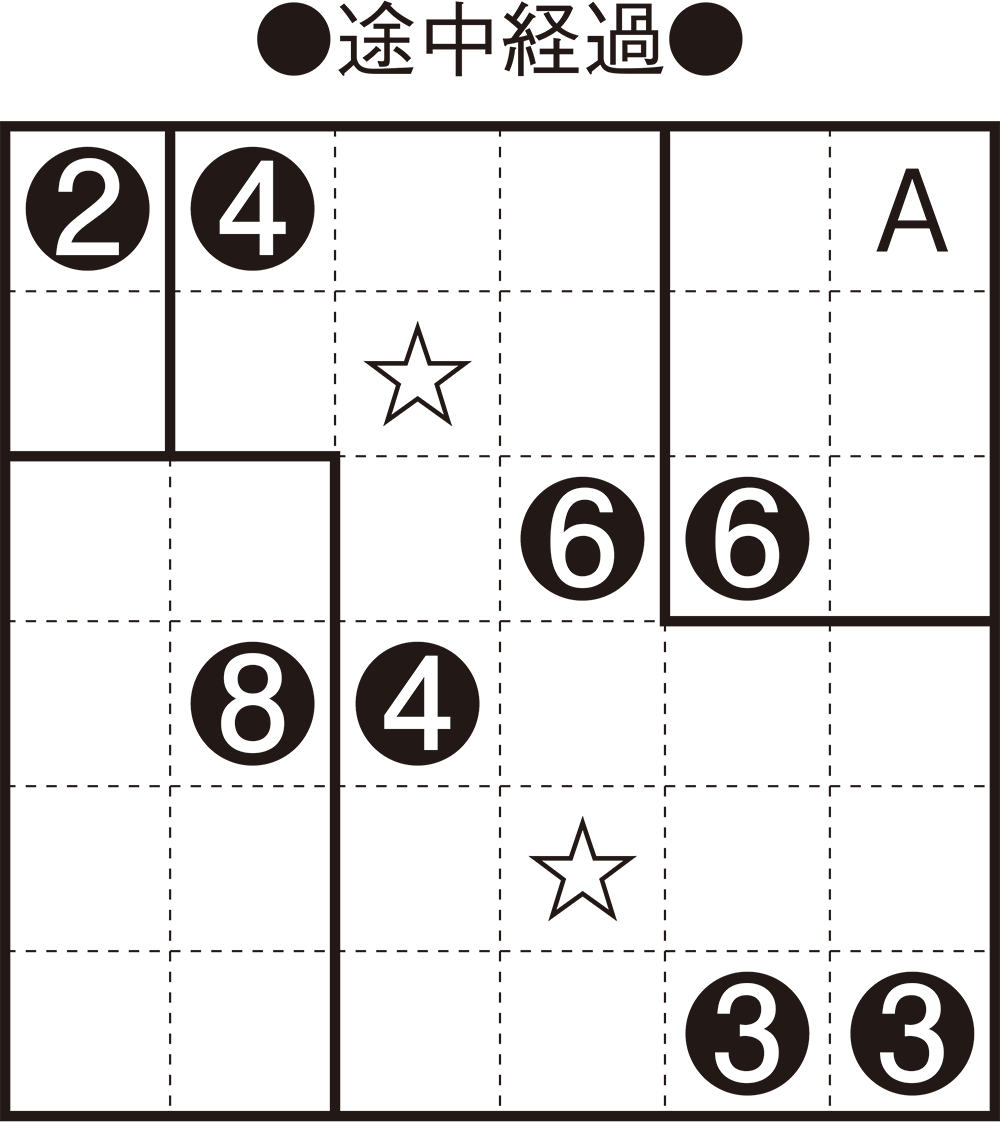
まず、盤面の左上にある「2」に注目しましょう。この「2」は途中経過のように、タテ長の長方形の中に入ります。すぐ右に「4」があるため、ヨコ長の長方形にはできないからです。
次に、盤面の左のほうの「8」が入る長方形について考えましょう。「8」が入る長方形は、1×8、2×4、4×2、8×1のいずれかになりますが、残っているスペースから、途中経過のように2×4のタテ長の長方形しか入らないことがわかりますね。
また、1つのマスに注目して解く方法もあります。途中経過のAのマスに注目してください。すべてのマスがどこかの長方形に入りますが、Aのマスを入れることができる数字は、右から2マス目、上から3マス目の「6」しかありません。よって、途中経過のようにAのマスを含むタテ長の長方形を書くことができます。
このように、長方形が1通りに決まるところを見つけながら、盤面全体を切り分けていきましょう。
【答え】
答え「16」