より深い学びを実現する『問題を改造して研究する』学習法

 

文系・理系を問わず一部のＺ会のスタッフに対して「Ｚ会に入社するまでに、問題を改造したこと（してみたいと思ったこと）はありますか？」というアンケートを実施したところ、「ある」と回答した人が78%を占めました。また、そのうちの約6割の人が、中学生・高校生の頃に問題の改造を試みていました。

Ｚ会のスタッフは学びに関わる仕事に携わっていますので、大学生のときに「人に教える」ために改題したことがあるという人も多かったのですが、中学生・高校生の頃から「定期テストの予想問題の作成」や「問題の構造の追究」のために問題を改造するという深い学びにつながる経験を積み重ねているという結果は興味深く感じます。

今回は、アンケートで最も多くの人が問題の改造を考えた教科である数学に焦点を当てて、数学の力をさらに伸ばすための学習法、名付けて『問題改造研究法』を紹介します。もちろん、英語やその他の教科でも有効な学習法ですので、試してみてくださいね。

なお、以前の記事では、数学の成績を伸ばすには「考え方を理解する」ことが大切であり、そのために「どうしてこの解法で解けるのだろう？」と理由を追究する姿勢を身につけてほしいということを、お伝えしております。こちらも合わせてご確認ください。

それでは、具体例とともに『問題改造研究法』についてご説明いたします。

例えば、「文字と式」（主に中学１年で学習する単元）では、次のような問題に取り組みますね。

この問題を解いた後は、「4つの数のうち1つの数を文字で表すと、ほかの3つの数も同じ文字を用いて表せる」や、「文字を用いて表すと、何の倍数になるかを調べやすい」のように、この問題が解ける理由を追究しましょう。そして、理由がわかったら『問題改造研究法』のスタートです。「4つの数の和が4の倍数」の代わりに、次のように問題を改造してみましょう。

1. 4つの数の積はどうなるだろうか？
2. 4つの数の和が8の倍数や12の倍数になることはないのだろうか？
3. 「1週間が6日間」のような変わったカレンダーでも「4つの数の和は4の倍数」がいえるのだろうか？
4. 2×2の枠で囲んだ4つの数の代わりに、3×3の枠で囲んだ9つの数にするとどうなるだろうか？

このように、自分で問題を改造して、答え（結論）がどのように変わるのか、研究してみてください。 1.を研究してみると、和と積では「○の倍数である」の説明のしかたが違ってくることに気づくでしょう。『問題改造研究法』は新たな気づきに出会うよいきっかけになりますよ。

もう1問、平面図形の面積を求める問題を例に挙げましょう。

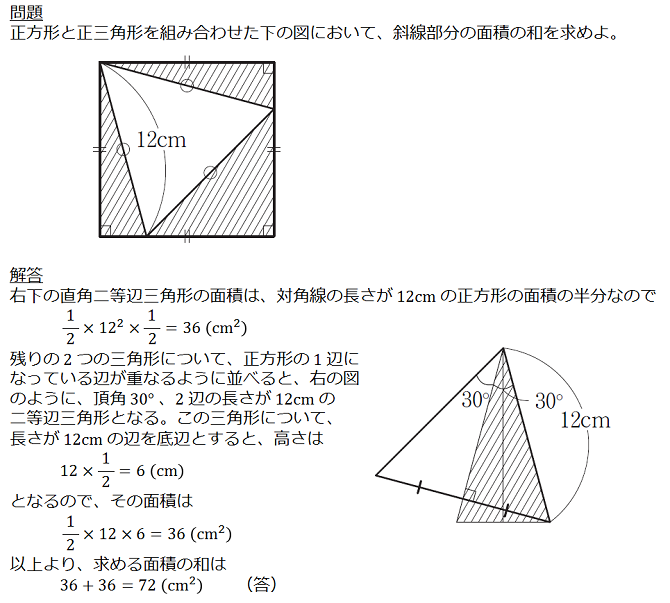
この問題を解くポイントは、特別な三角形（直角二等辺三角形や、3つの角が30°、60°、90°の三角形）の辺の比を活用することですね（三平方の定理や三角比を用いて解くこともできます）。そして、この問題では正方形の中に正三角形がありますが

1. 正方形と正三角形を逆にした、正三角形の中に正方形がある場合はどうなるだろうか？
2. 正三角形や正方形を、正五角形や正六角形などに変えるとどうなるだろうか？

のように、問題を改造してみるとどうでしょうか。図形を少し変えただけですが、改造した問題を解くためには、実は、もとの問題よりも幅広い知識が必要になります。

問題の改造のしかたによっては、解くのに必要となる知識をまだ習得していないために、解けない問題へと改造してしまうかもしれない、ということですね（もしかしたら、最先端の数学でも未解決な問題になるかもしれません）。

「解けないかもしれない問題を考えることに何の意味があるのか？」と思われるかもしれませんが、「この問題は、○○だから、今の自分には解けない」と根拠を添えて判断できるようになることは、数学の力をさらに伸ばすうえで非常に重要です。『問題改造研究法』を実践することで、自分が持っている知識や、その知識で解ける範囲を、点検・整理することができますし、さらに知識を広げていく先を感じることができます。

普段の学習では、それまでに学んだ知識・考え方を用いれば必ず解ける問題しか出題されません。しかし、解けることが保証されている問題の演習だけでは、答えのない社会の問題解決の練習にはほど遠いものになります。将来使える本当の数学力を育成するために、週に1度や、月に1度は、『問題改造研究法』で「解けないかもしれない問題」について研究してみませんか？

Ｚ会Asteria数学新系統講座では、皆様の「研究ノート」をお待ちしております。ご提出いただいた「研究ノート」には、次の学びへとつながるコメントを添えてお返事いたします。

Ｚ会Asteria数学新系統講座では、

• 理由の追究に適した問題と解説を豊富に収録したTraining（問題演習）
• 考え方がきちんと理解できているかを確認できるBrush Up（添削課題）
• 自分で考えた理由が合っているのかを質問できるDiscovery Note（質問回答）

を通して、より深い学習ができます。「Discovery Note」を通じて「研究ノート」を提出してみましょう。

新大学入試で用いられる語学力の国際指標「CEFR（セファール）」基準で、4技能をバランスよく伸ばせる「英語４技能講座」、統計を含む分野別学習で学ぶ「数学新系統講座」。オンラインで他の受講生と主体的・対話的で深い学び（いわゆる、アクティブ・ラーニング）を実現した「総合探究講座」。知識に加え、社会で必要な力が問われる新入試に向けた一朝一夕では身につかない力を育めます。

iPad１台に深淵な学びの世界を凝縮したＺ会Asteriaが、未来に向けて進むあなたを導きます。
※受講にはiPadが必要です。