公開日:2018/01/18

「知識のつながり」の大切さ
大学入学共通テストでは、評価すべき能力として、「数学を活用した問題解決に向けて構想・見通しを立てること」に関わる能力が挙げられています。つまり、従来の試験よりも一層、知識を活用する力が問われており、暗記しただけの知識は求められていません。そこで、それぞれの知識をばらばらに覚えるのではなく、複数の知識を関連付けながら理解を深めていく「学び」がカギとなってきます。
【 3個の知識より10個の知識】
たとえば、3個の知識と10個の知識、どちらの方が楽に理解できるでしょうか。「数が少ない方がすぐに覚えられる」と思うかもしれませんが、覚えることと理解することは違います。多くの知識を関連付けながら確認していくことで、理解をどんどん深めていくことができますし、そのようにして身につけた知識は決して忘れることはありません。
例として、四角形を取り上げてみます。
●3個の知識の場合の例
●10個の知識(のネットワーク)の場合の例
例として、四角形を取り上げてみます。
●3個の知識の場合の例
- 2組の対辺がそれぞれ平行な四角形を平行四辺形という。
- 4つの内角が等しい四角形を長方形という。
- 4つの辺が等しい四角形をひし形という。
●10個の知識(のネットワーク)の場合の例
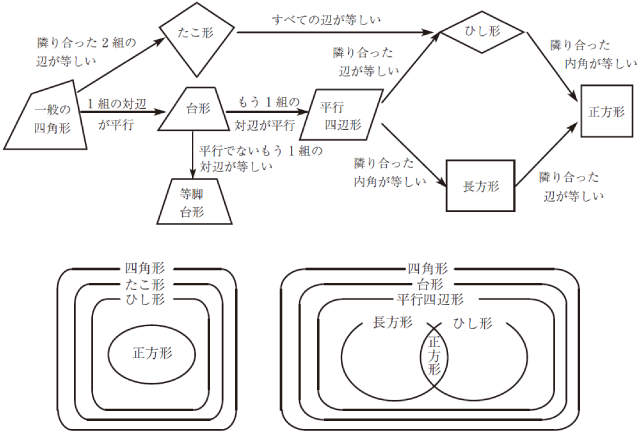
「3個の知識よりも10個の知識の方が理解しやすい」という話について、さまざまな四角形に関する知識を例に、もう一度考えてみましょう。
平行四辺形、長方形、ひし形という3つの四角形の名前とその定義を覚えるだけであれば難しくないかもしれません。では、10個、100個、……、とたくさんの知識を覚えられるでしょうか。そして、ずっと覚え続けていられるでしょうか。そんなことは不可能ですし、そもそも意味がありません。そのようにして覚えただけの知識は、活用することができないからです。
四角形に関する複数の知識のつながりの例を挙げると、上の図のようになるでしょう。台形、平行四辺形、長方形、ひし形、正方形、……。これらの四角形はそれぞれ関係し合いながら定義されており、その関係性にも意味があります。その関係性に着目し、意味を理解することこそ、学ぶべき事柄でしょう。つまり、知識はメモではなくネットワークなのです。メモは散らかっていくと収拾がつかなくなりますが、ネットワークは広がるほど充実していきます。知識のネットワークを充実させることが「学び」であり、それによって理解が深まり、活用できるようになるのです。
平行四辺形、長方形、ひし形という3つの四角形の名前とその定義を覚えるだけであれば難しくないかもしれません。では、10個、100個、……、とたくさんの知識を覚えられるでしょうか。そして、ずっと覚え続けていられるでしょうか。そんなことは不可能ですし、そもそも意味がありません。そのようにして覚えただけの知識は、活用することができないからです。
四角形に関する複数の知識のつながりの例を挙げると、上の図のようになるでしょう。台形、平行四辺形、長方形、ひし形、正方形、……。これらの四角形はそれぞれ関係し合いながら定義されており、その関係性にも意味があります。その関係性に着目し、意味を理解することこそ、学ぶべき事柄でしょう。つまり、知識はメモではなくネットワークなのです。メモは散らかっていくと収拾がつかなくなりますが、ネットワークは広がるほど充実していきます。知識のネットワークを充実させることが「学び」であり、それによって理解が深まり、活用できるようになるのです。
【新たな知識を学習するときは…】
数学の学習において、とくに新しい単元で今まで知らなかった概念に触れるとき、その知識を理解することばかりに目がいってしまうかもしれません。
たとえば、「三角比」の単元で余弦定理を学習すると、余弦定理の式を覚えたり使い方を練習したりといったことにとらわれがちです。もちろんそういった演習も大切なのですが、より重要なことは「既に知っている知識と新たに知った知識のつながり」です。言い換えると「新たに知った知識を追加して、知識のネットワークを広げること」が肝要だということです。
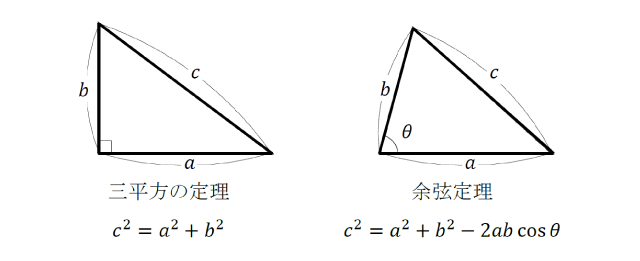
余弦定理を学習する際には、既に学習した三平方の定理との関係性に思いをはせて、
・三平方の定理も余弦定理も、三角形の3辺の長さに関する定理である
・三平方の定理は直角三角形にしか適用できないが、余弦定理はどのような三角形にも適用することができる
といった共通点や違いを意識して捉えることがポイントなのです。
たとえば、「三角比」の単元で余弦定理を学習すると、余弦定理の式を覚えたり使い方を練習したりといったことにとらわれがちです。もちろんそういった演習も大切なのですが、より重要なことは「既に知っている知識と新たに知った知識のつながり」です。言い換えると「新たに知った知識を追加して、知識のネットワークを広げること」が肝要だということです。
余弦定理を学習する際には、既に学習した三平方の定理との関係性に思いをはせて、
・三平方の定理も余弦定理も、三角形の3辺の長さに関する定理である
・三平方の定理は直角三角形にしか適用できないが、余弦定理はどのような三角形にも適用することができる
といった共通点や違いを意識して捉えることがポイントなのです。
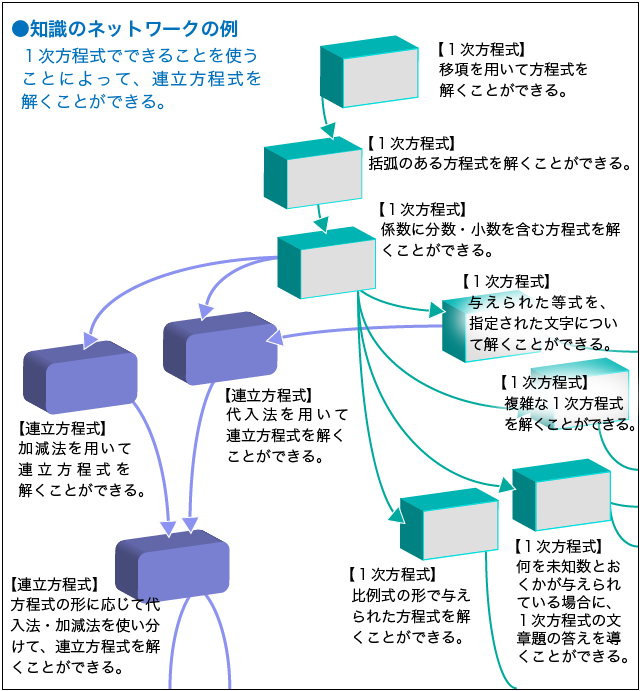
そのように学んでいけば、「余弦定理の式は複雑でよくわからない」、「余弦定理をいつ使えばよいのかわからない」といった悩みに苦しむことは決してありません。
未来を共創する21世紀型Online Academy Z会Asteria

新大学入試で用いられる語学力の国際指標「CEFR(セファール)」基準で、4技能をバランスよく伸ばせる「英語4技能講座」、統計を含む分野別学習で学ぶ「数学新系統講座」。オンラインで他の受講生と主体的・対話的で深い学び(いわゆる、アクティブ・ラーニング)を実現した「総合探究講座」。知識に加え、社会で必要な力が問われる新入試に向けた一朝一夕では身につかない力を育めます。※受講にはiPadが必要です。