POST-READING
EXTRACTING THE MAIN IDEA
Which of the following is the most appropriate as the main idea of the passage?
- Some probability problems show us that it is not good to depend too much on our intuition.
- The probability that there will be a matching date of birth in a randomly selected group is greater than expected.
- Some probability problems have truly counterintuitive results. They not only help us understand the deep meaning of probability, but are also very enjoyable.
- To reach the correct conclusion, we should look at the entire situation as a step-by-step process.
SHARING YOUR OPINION
MORE! SHARING YOUR OPINION
Working in pairs, share your opinions about the following questions.
Question A If you were a contestant in Let’s Make a Deal, would you stay with your original choice of door after one of the remaining doors was opened?
Question B When you make a decision, do you follow your intuition, or take probability into account?
 Useful Words or Phrases
Useful Words or Phrases
- 〜を考慮に入れる take 〜 into account(= take account of 〜)
- 〜を成し遂げる achieve 〜
- 〜を後悔する;後悔 regret
- 〜を危険にさらす,賭ける risk 〜
- データ data
- 財産を成す make a fortune
CHECKING THE FRAMEWORK
Fill in the blanks, selecting from a ~ f below the most appropriate title for each section. Also check how the sections and paragraphs relate to each other.
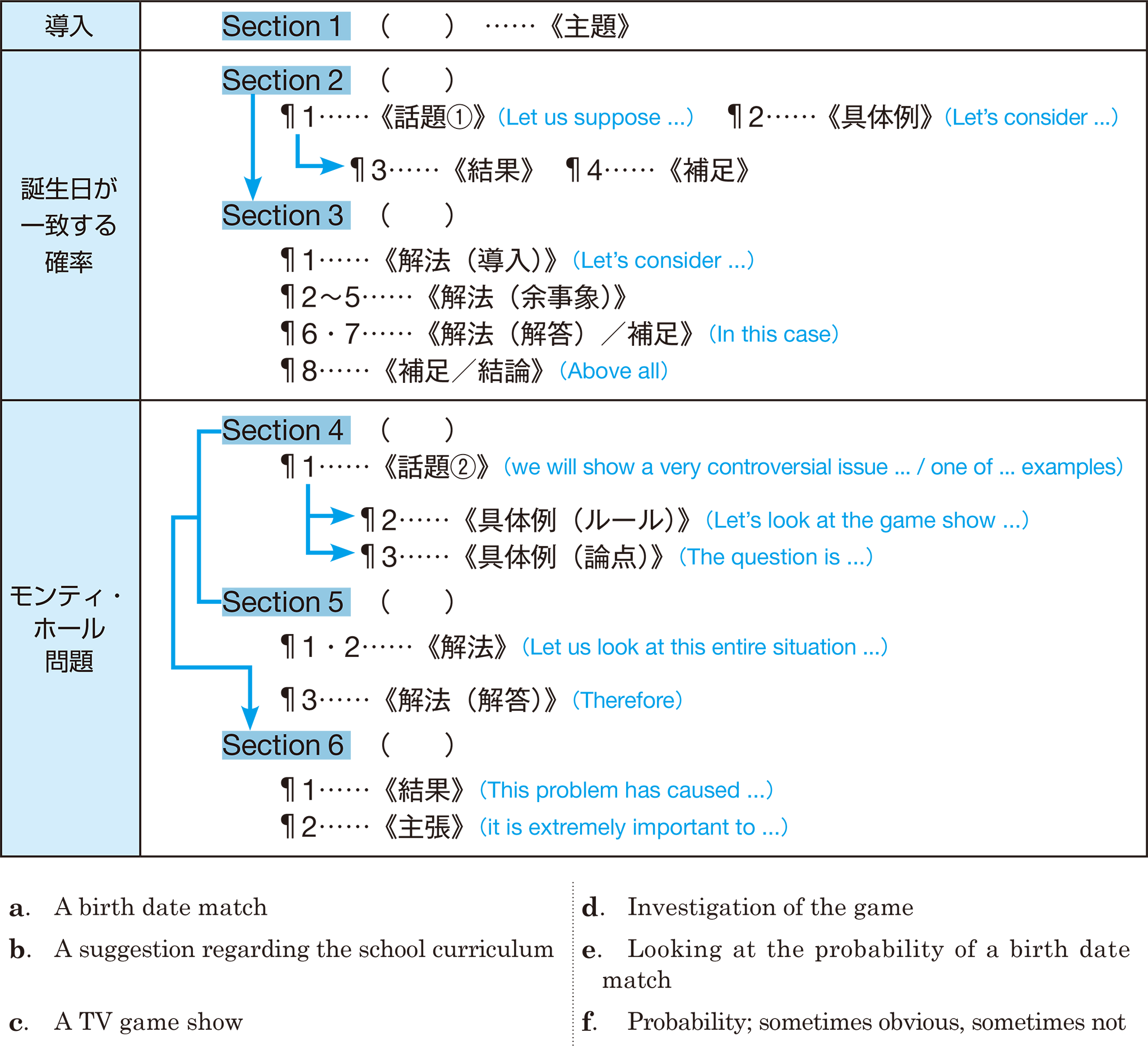
SUMMARY
Fill in the blanks, thinking back to the answer to the question following each section numbers. Read the finished summary aloud.

Probability produces results that are sometimes ①(intuitively logical) and sometimes truly counterintuitive, as follows. For example, when asked what the probability is that two of a random group of thirty-five people have the same birth date, you may intuitively think that the probability is minuscule, but actually, the probability is ②(greater than 8 out of 10). So, the author says that it is not good to ③(rely too much on your intuition). The game show Let’s Make a Deal is also introduced as a ④(counterintuitive example) that gives a deeper meaning to understanding the concept of probability. In this game, ⑤(the logical decision) helps improve the chance of winning. The author suggests that this problem should be a part of the school curriculum in order to make probability not only more ⑥(understandable but also more enjoyable).