Fortunately, the topic of probability is becoming ever more popular in the school curriculum today. Most of the results are intuitively logical (e.g., the probability of flipping a coin and getting a head is one half; the probability of throwing a die to get a 2 is one-sixth; and so on). We also know that the probability of winning a lottery is rather small, but yet there are some results in the field of probability that are truly counterintuitive. Here we will present a situation that could be described as one of the most surprising results in mathematics. It is one of the best ways to convince the uninitiated of the “power” of probability. We hope with this example not to upset your sense of intuition.

Let us suppose you are in a room with about thirty-five people. What do you think the chances are (or the probability is) that two of these people have the same birth date (month and day only)? Intuitively, you usually begin to think about the likelihood of 2 people having the same date out of a selection of 365 days (assuming no leap year). Perhaps 2 out of 365? That would be a probability of %. A minuscule chance.

Let’s consider the “randomly” selected group of the first thirty-five presidents of the United States. You may be astonished that there are two with the same birth date: the eleventh president, James K. Polk (November 2, 1795), and the twenty-ninth president, Warren G. Harding (November 2, 1865).

You may be surprised to learn that for a group of thirty-five, the probability that two members will have the same birth date is greater than 8 out of 10, or ＝80%.

If you have the opportunity, you may wish to try your own experiment by selecting ten groups of about thirty-five members to check on date matches. For groups of thirty, the probability that there will be a match is greater than 7 out of 10, or, in other words, in 7 of these 10 groups there ought to be a match of birth dates. What causes this incredible and unanticipated result? Can this be true? It seems to be counterintuitive.

To relieve you of your curiosity, we will investigate the situation mathematically. Let’s consider a class of thirty-five students. What do you think is the probability that one selected student matches his own birth date? Clearly certainty, or 1. This can be written as .

The probability that another student does not match the first student is .

The probability that a third student does not match the first and second students is .

The probability of all thirty-five students not having the same birth date is the product of these probabilities: .

Since the probability (q) that two students in the group have the same birth date and the probability (p) that two students in the group do not have the same birth date is a certainty, the sum of those probabilities must be 1. Thus, p+q=1.

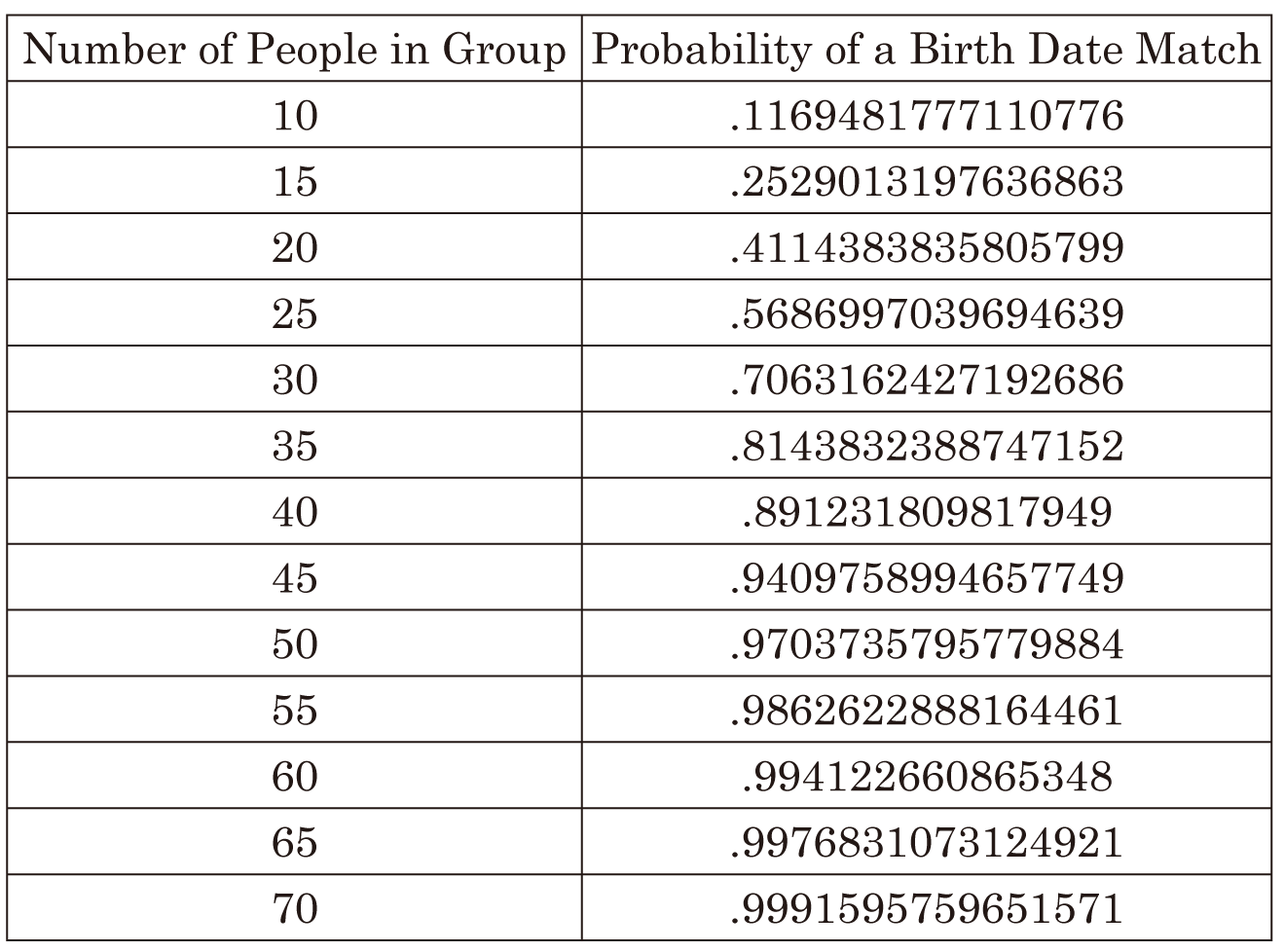
In this case, In other words, the probability that there will be a birth date match in a randomly selected group of thirty-five people is somewhat greater than . This is quite unexpected when you consider that there were 365 dates from which to choose. If you are feeling motivated, you may want to investigate the nature of the probability function. Here are a few values to serve as a guide:

Notice how quickly “almost-certainty” is reached. With about 55 students in a room the chart indicates that it is almost certain (.99) that two students will have the same birth date.

Were you to do this with the death dates of the first thirty-five presidents, you would notice that two died on March 8 (Millard Fillmore in 1874 and William H. Taft in 1930) and three presidents died on July 4 (John Adams and Thomas Jefferson in 1826, and James Monroe in 1831). This latter case leads some people to argue that you could possibly will your own date of death, since these three presidents died on the most revered day in American history! Above all, this astonishing demonstration should serve as an eye-opener about the inadvisability of relying too much on your intuition.

While the previous unit showed us that some probability results are quite counterintuitive, here we will show a very controversial issue in probability that also challenges our intuition. There is a rather famous problem in the field of probability that is typically not mentioned in the school curriculum, yet it has been very strongly popularized in newspapers, magazines and even has at least one book entirely devoted to the subject. It is one of these counterintuitive examples that gives a deeper meaning to understanding the concept of probability.

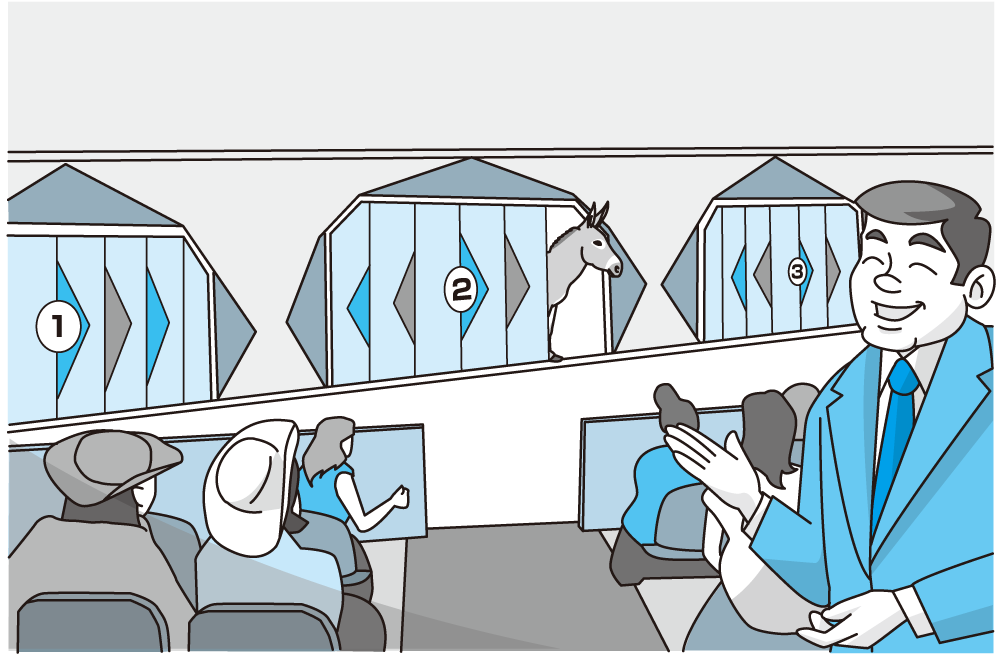
This example stems from the long-running television game show Let’s Make a Deal, which featured a rather curious problematic situation. Let’s look at the game show in a simplified fashion. As part of the game show, a randomly selected audience member would come on stage and be presented with three doors. She was asked to select one, with the hope of selecting the door that had a car behind it, and not one of the other two doors, each of which had a donkey behind it. Selecting the door with the car allowed the contestant to win the car. There was, however, an extra feature in this selection process. After the contestant made her initial selection, the host, Monty Hall, exposed one of the two donkeys, which was behind a not-selected door —— leaving two doors still unopened, the door chosen by the contestant and one other door. The audience participant was asked if she wanted to stay with her original selection (not yet revealed) or switch to the other unopened door. At this point, to heighten the suspense, the rest of the audience would shout out “stay” or “switch” with seemingly equal frequency.

The question is, what to do? Does it make a difference? If so, which is the better strategy to use here (i.e., which offers the greater probability of winning)? Intuitively, most would say that it doesn’t make any difference, since there are two doors still unopened, one of which conceals a car and the other a donkey. Therefore, many folks would assume there is a 50/50 chance that the door the contestant initially selected is just as likely to have the car behind it as the other unopened door.

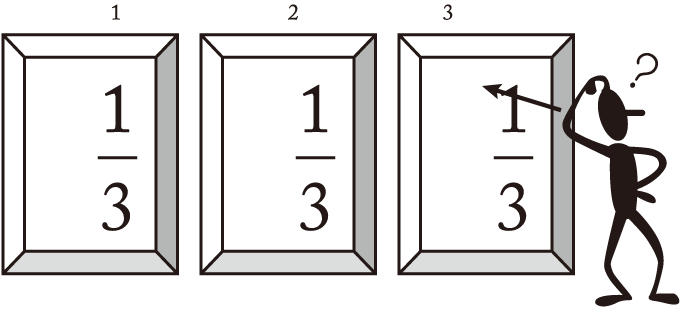
Let us look at this entire situation as a step-by-step process, and then the correct response should become clear. There are two donkeys and one car behind these three doors. The contestant must try to get the car. Let’s assume that she selects Door 3. Using simple probabilistic thinking, we know the probability that the car is behind Door 3 is . Therefore, the probability that the car is behind either Door 1 or Door 2 is then . This is important to remember as we move along.

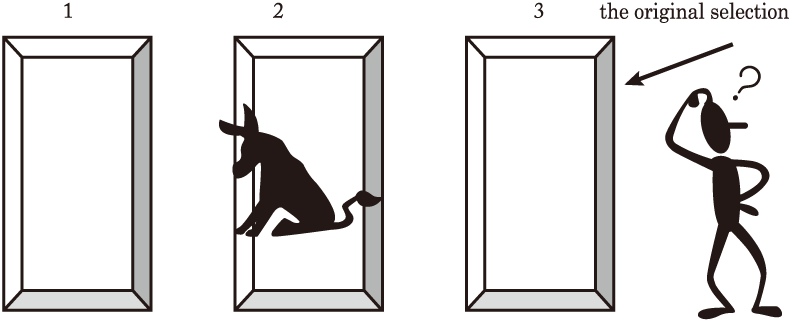
Knowing where the car is hidden, host Monty Hall then opens one of the two doors that the contestant did not select, and exposes a donkey. Let’s say that the contestant chose Door 3 and Monty revealed Door 2 (with a donkey). Keep in mind that the probability that the car is behind one of these two remaining doors, Doors 1 and 2, is .

He then asks the contestant, “Do you still want your first-choice door, or do you want to switch to the other closed door?” Remember, as we said above, the combined probability of the car being behind Door 1 or Door 2 is . Now with Door 2 exposed as not having the car behind it, the probability that the car is behind Door 1 is still , while we recall the probability that the car is behind Door 3, the door initially selected by the contestant, is still only . Therefore, the logical decision for the contestant is to switch to Door 1. (Door 1’s probability for having the car is ; Door 3’s is the lesser .)

This problem has caused many an argument in academic circles, and it was also a topic of discussion in the New York Times, as well as other popular publications.

Although this is a very entertaining and popular problem, it is extremely important to understand the message herewith imparted; and it is one that by all means should have been a part of the school curriculum to make probability not only more understandable but also more enjoyable.