新中1生〜新高2生必見！共通テスト試行調査から見えるもの〜数学で求められる力とは？〜

先日、大学入試センターは大学入学共通テスト（現行のセンター試験に代わって2020年度から実施予定）の導入に向けた平成30年度（2018年度）試行調査の問題と解答を公表しました。
試行調査は平成29年度に続けて2回目の実施となり、昨年度の試行調査に比べ、各教科で具体的に見えてきたものがありました。共通テストの試行調査から、どのようなメッセージが読み取れるでしょうか？そして、今からどのような学習を行っていけばよいでしょうか？

今回は、数学の試行調査問題の3つの特徴
  1. 計算問題が少ない！
  2. 誘導が少ない！
  3. 活用を重視！
に焦点を当てつつ、この共通テストを受けることになる、2019年4月時点で高校2年生までのみなさんが今から取り組むべき学習について説明します。

 

1. 計算問題が少ない！

「数学I・数学A」の問題を解き進めていくと、計算問題が少ないことに驚きます。現行のセンター試験と比べて大幅に多い29ページの問題冊子において、11ページ目までほとんど計算は必要ありません。すべての問題を見渡してみても、複雑な計算が必要となる問題はあまり多くありません。

特に、「数学I・数学A」第1問〔2〕（リンク先問題冊子 pp.6〜7）の二次関数に関する問題では、まったく計算せずに答えを導くことができます。大学入試センターが公開している「問題のねらい、主に問いたい資質・能力及び小問の概要等」では、この問題は「二次関数のグラフを変化させたときに、二次方程式や二次不等式の解がどのように変化するかを、計算をせずに考察する問題」であり、「数学的な見方・考え方を基に的確かつ能率的に処理する力や、得られた結果を基に体系的に整理する力を問う」ために出題していることがわかります。

具体的には、この問題では
  • 関数f(x)=a(x-p)2+q においてa、p、q の値を変化させるとy=f(x)のグラフはどのように変化するのか
  • そのグラフの形と、方程式f(x)=0や不等式f(x)>0の解との間には、どのような関係があるのか
という内容を考えることになります。二次関数のグラフの特徴がきちんと理解できているかを確認するための問題というわけです。
単に公式を覚えたり問題の解き方を暗記したりすることができているかではなく、数学的な考え方を身につけられているかどうかが問われ、考え方を重視した内容となっています。

2. 誘導が少ない！

前節では共通テスト全体として計算問題が少ないことをお伝えいたしましたが、もちろん計算が必要となる問題も一部あります。とはいえ、求められているのは公式に当てはめて計算を行う力ではありません。どの公式を使うのかを自分で判断したり、公式を使うための準備として文字を設定したり、といった答えに至るまでの流れを組み立てる力が必要となるのです。

このことは、大学入試センターの資料では「構想・見通しを立てること、目的に応じて数・式、図、表、グラフなどを活用し、一定の手順に従って数学的に処理すること」と表現されています。

「数学I・数学A」第2問〔1〕（リンク先問題冊子 pp.12〜13）を例に、この力についてもう少し考えてみましょう。この問題では、直角三角形の辺上を3つの点が動くときの、線分の長さや三角形の面積の変化について考察することがテーマとなっています。この問題の(1)の問いを正しく解くためには
  • 時刻t などの文字を自分で設定する
  • 線分の長さや三角形の面積を、文字を用いて自分で立式する
  • (1)(ii)では、グラフを活用して、線分の長さが指定された値をとる回数を判断する
という流れをすべて自分で組み立てなければなりません。

そして、(2)では、(1)とは別の直角三角形の面積について考えることになり、ここでは
  • (1)の答えを導いた過程を振り返り、(2)の直角三角形の場合に応用する
のように、自分で答えを求めるための方針を立てることが求められます。
解答を組み立てる力・振り返る力を身につけるためには、普段の学習でも「この公式を使えば何を求めることができるのか」や「この公式はどのようなときに有効なのか」といったことを意識することが大切です。

3. 活用を重視！

前節でも、式やグラフといった「道具の活用」という文脈で「活用」というキーワードが出てきていますが、学習指導要領解説ではもう1つの観点で「活用」という言葉が使われています。それは「知識の活用」であり、「新たに得られた知識などをこれまで得られていた知識などと合わせ、批判的に検討することにより、知識などを体系的に整理することができ、様々な場面で活用する」と書かれています。

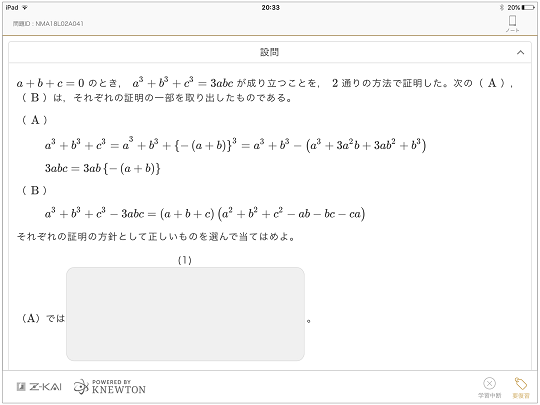
たとえば、「数学I・数学A」第5問（リンク先問題冊子 pp.26〜29）は、三角形の各頂点からの距離の和が最小となる点（フェルマー点とよばれます）の性質の証明に関する問題であり、証明の過程で必要となる定理が問題文で与えられています。知っている知識（教科書に載っている知識）をもとに、問題文で与えられた定理を用いて証明を補うことで、フェルマー点の性質（教科書に載っていない発展的な知識）へと結びつけて活用すること。これがこの問題で試されている力であり、単に平面図形に関する知識だけが問われているわけではないということですね。

新高校2年生までの方が取り組むべき学習とは？

これまでに述べてきたポイントをまとめると
  • 数学的な考え方を身につけること
  • 自力で解答を組み立てる力を身につけること
  • 知識を活用するために体系的に整理すること
の3つが共通テストに向けた学習の目標となります。
この目標を達成するための学習方法は、一つひとつの知識に対して「どうしてこのように考えるのだろうか」と追究してより深く理解すること。
そして、問題演習を積み重ねる中で「あの問題もこの問題も○○○だから、どちらも●●●を使うことができる」や「あの問題とこの問題は□□□が違うから、あの問題は▲▲▲だけどこの問題は■■■になる」のように、知識のつながりを見いだして体系化していくこと。

上に示した映像講義・問題のサンプルのように、「Ｚ会Asteria数学新系統講座」には
  • 知識を深く理解するための映像講義
  • 知識を体系化するための豊富な問題演習
  • 知識を活用する力を鍛えるための添削課題
があります。本講座を通して、効率よく知識を習得し、数学的な見方・考え方が身についていく喜びを感じていただけることを願っています。

英語４技能、数学の記述問題、協働学習　−　一歩先を行く人のための学び場がここに

新大学入試で用いられる語学力の国際指標「CEFR（セファール）」基準で、4技能をバランスよく伸ばせる「英語４技能講座」、統計を含む分野別学習で学ぶ「数学新系統講座」。オンラインで他の受講生と主体的・対話的で深い学び（いわゆる、アクティブ・ラーニング）を実現した「総合探究講座」。知識に加え、社会で必要な力が問われる新入試に向けた一朝一夕では身につかない力を育めます。

iPad１台に深淵な学びの世界を凝縮したＺ会Asteriaが、未来に向けて進むあなたを導きます。
※受講にはiPadが必要です。

公開日：2019/01/23
最終更新日：2019/03/07