中高一貫校に通う、中学3年生の皆さまへ〜数学編〜

 

皆さんは、中学範囲の数学をきちんと理解して学習を進めることができているでしょうか。一般的に一貫校の学習進度は公立校と比べて速いので、既に高校範囲の数学の学習が始まっている学校もあるかと思います。そのような中で、もしかしたら「きちんと理解する前に次の単元に進んでしまう」、「十分に復習する時間がとれない」という悩みを抱えている人もいるのではないでしょうか。
そこで、高校範囲の数学が本格化する前に確実にできるようになっておきたい中学数学の単元を3つ、厳選してお伝えいたします。いずれも、高校数学につながる大切な単元ですので、きちんと理解できているかチェックして、必要ならば復習しておきましょう。

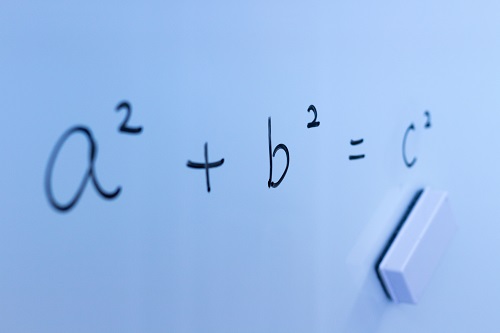
三平方の定理は、直角三角形の辺の長さを求めることができる非常に強力な定理であり、この定理を中心にさまざまな図形の線分の長さ・面積について考えるこの単元は、中学範囲の図形分野の集大成と言えるでしょう。この三平方の定理をスタート地点として、より一般的な図形を扱うのが、高校数学で学ぶ「三角比」であり、これがさらには「ベクトル」へとつながっていきます。
高校数学の図形分野をマスターする基礎となる「三平方の定理」を自在に使いこなせるようになっておきましょう。

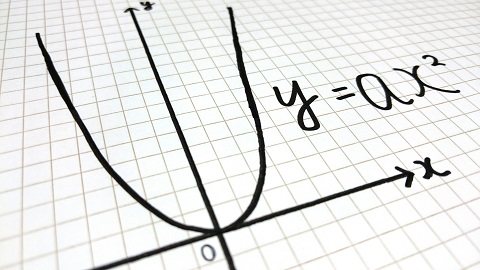
中学数学で扱う主な関数といえば「1次関数」と「2乗に比例する関数」。とくに、 x と y の対応がより複雑な「2乗に比例する関数」の学習を通じて

• x の値が変化したときに y の値はどのように変化するか
• x がどのような値のときに y の値が最大となるか

といった、 x と y の関係性に着目する関数の考え方や

• 2つの関数のグラフの交点の座標は何か

といった関数の式の扱い方を身につけておくことは、高校数学で出てくる「2次関数」や「三角関数」、「指数関数・対数関数」などの重要な関数をスムーズに理解する上で大きな強みとなるでしょう。

高校数学では、中学数学に比べて高度な内容になり、よりハイレベルな計算力が必要となります。数学を学ぶ上で、計算力をつねに鍛え上げていくことは欠かせません。とくに、中学の「式の計算」で学ぶ展開・因数分解は、高校の「数と式」の単元と直結しており、その先の「整式の除法」や「等式・不等式の証明」を初めとする多くの単元で必要となるものです。
展開・因数分解などの計算をミスせずに素早く行ったり、計算量が減るような工夫をしたりすることに不安がある人は、今のうちに自分のミスの傾向を把握して克服し、計算力を高めておきましょう。

Ｚ会Asteria数学新系統講座では、一人ひとりの学習の理解度に応じて次に取り組むのに適した課題を提示する「アダプティブ・ラーニング」と呼ばれる仕組みを採用しています。もしも自分では気づいていない苦手があったとしても見逃さず、理解が十分になるまできっちり学習できるのです。
自分の得意・不得意に合わせて、確実に理解できるまで反復して問題演習に取り組むことができるので、効率よく復習したい方には、Ｚ会Asteria数学新系統講座がオススメです。

新大学入試で用いられる語学力の国際指標「CEFR（セファール）」基準で、4技能をバランスよく伸ばせる「英語４技能講座」、統計を含む分野別学習で学ぶ「数学新系統講座」。オンラインで他の受講生と主体的・対話的で深い学び（いわゆる、アクティブ・ラーニング）を実現した「総合探究講座」。知識に加え、社会で必要な力が問われる新入試に向けた一朝一夕では身につかない力を育めます。

iPad１台に深淵な学びの世界を凝縮したＺ会Asteriaが、未来に向けて進むあなたを導きます。
※受講にはiPadが必要です。