数学の問題を例に知識のつながりを考える_2018.3
公開日 2018.3.14
2020年度から実施される「大学入学共通テスト(共通テスト)」では、知識をつなげることが重要視されます。
例えば、文部科学省は大学入学共通テストの数学の「評価すべき項目」として、「数学を活用した問題解決に向けて構想・見通しを立てること」を挙げています。つまり、知識を覚えることに留まらず、理解し、問題を解決するためにつなぎ合わせる必要があるのです。しかし、知識をつなげるとはどういうことなのでしょうか。今回の記事では、数学の問題を例に考えていきます。
例えば、文部科学省は大学入学共通テストの数学の「評価すべき項目」として、「数学を活用した問題解決に向けて構想・見通しを立てること」を挙げています。つまり、知識を覚えることに留まらず、理解し、問題を解決するためにつなぎ合わせる必要があるのです。しかし、知識をつなげるとはどういうことなのでしょうか。今回の記事では、数学の問題を例に考えていきます。
◆3個の知識と10個の知識
3個の知識と10個の知識、どちらの方が楽に理解できるでしょうか。「数が少ない方がすぐに覚えられる」と思うかもしれませんが、覚えることと理解することは違います。多くの知識を関連付けながら確認していくことで、理解をどんどん深めていくことができますし、そのようにして身につけた知識は決して忘れることはありません。
例として、四角形を取り上げてみます。
●3個の知識の場合の例
●10個の知識(のネットワーク)の場合の例
例として、四角形を取り上げてみます。
●3個の知識の場合の例
- 2組の対辺がそれぞれ平行な四角形を平行四辺形という。
- 4つの内角が等しい四角形を長方形という。
- 4つの辺が等しい四角形をひし形という。
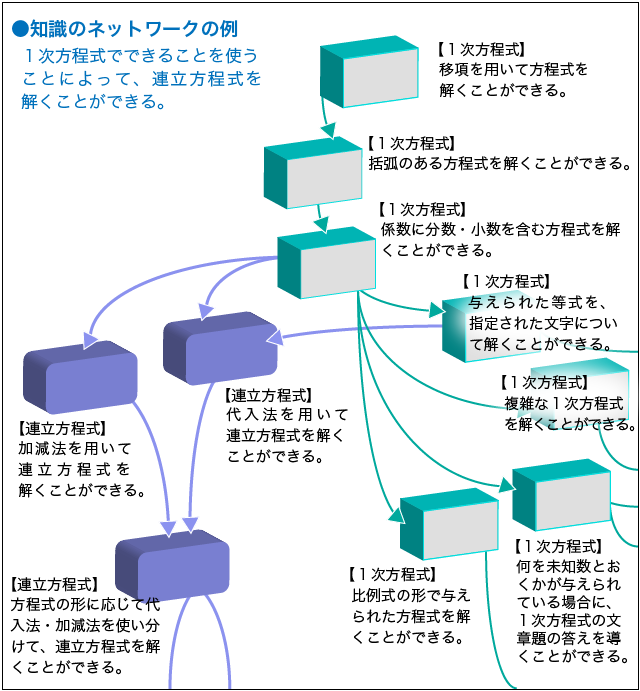
●10個の知識(のネットワーク)の場合の例
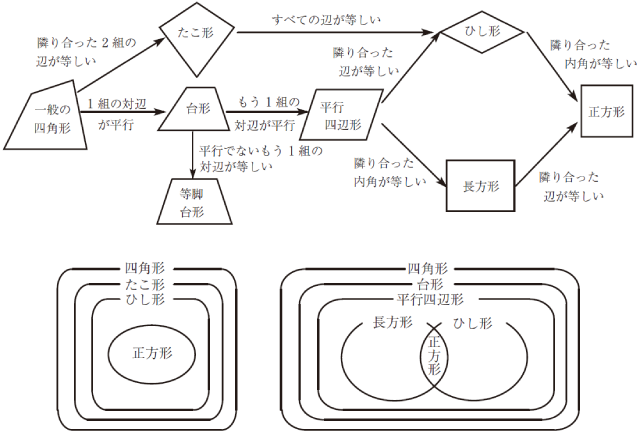
「3個の知識よりも10個の知識の方が理解しやすい」という話について、さまざまな四角形に関する知識を例に、もう一度考えてみましょう。
平行四辺形、長方形、ひし形という3つの四角形の名前とその定義を覚えるだけであれば難しくないかもしれません。では、10個、100個、……、とたくさんの知識を覚えられるでしょうか。そして、ずっと覚え続けていられるでしょうか。そんなことは不可能ですし、そもそも意味がありません。そのようにして覚えただけの知識は、活用することができないからです。
ここでは、四角形に関する複数の知識のつながりを図にして整理しました。台形、平行四辺形、長方形、ひし形、正方形、……。これらの四角形はそれぞれ関係し合いながら定義されており、その関係性にも意味があります。その関係性に着目し、意味を理解することこそ、学ぶべき事柄でしょう。つまり、知識はメモではなくネットワークなのです。メモは散らかっていくと収拾がつかなくなりますが、ネットワークは広がるほど充実していきます。知識のネットワークを充実させることが「学び」であり、それによって理解が深まり、活用できるようになるのです。
大学入学共通テストで評価される「数学を活用した問題解決に向けて構想・見通しを立てること」に関わる能力を身につけるには、このようにそれぞれの知識をばらばらに覚えるのではなく、複数の知識を関連付けながら理解を深めていく「学び」がカギとなってくるでしょう。
平行四辺形、長方形、ひし形という3つの四角形の名前とその定義を覚えるだけであれば難しくないかもしれません。では、10個、100個、……、とたくさんの知識を覚えられるでしょうか。そして、ずっと覚え続けていられるでしょうか。そんなことは不可能ですし、そもそも意味がありません。そのようにして覚えただけの知識は、活用することができないからです。
ここでは、四角形に関する複数の知識のつながりを図にして整理しました。台形、平行四辺形、長方形、ひし形、正方形、……。これらの四角形はそれぞれ関係し合いながら定義されており、その関係性にも意味があります。その関係性に着目し、意味を理解することこそ、学ぶべき事柄でしょう。つまり、知識はメモではなくネットワークなのです。メモは散らかっていくと収拾がつかなくなりますが、ネットワークは広がるほど充実していきます。知識のネットワークを充実させることが「学び」であり、それによって理解が深まり、活用できるようになるのです。
大学入学共通テストで評価される「数学を活用した問題解決に向けて構想・見通しを立てること」に関わる能力を身につけるには、このようにそれぞれの知識をばらばらに覚えるのではなく、複数の知識を関連付けながら理解を深めていく「学び」がカギとなってくるでしょう。
◆新たな知識を学習するときは…
数学の学習において、とくに新しい単元で今まで知らなかった概念に触れるとき、その知識を理解することばかりに目がいってしまうかもしれません。
たとえば、「三角比」の単元で余弦定理を学習すると、余弦定理の式を覚えたり使い方を練習したりといったことにとらわれがちです。もちろんそういった演習も大切なのですが、より重要なことは「既に知っている知識と新たに知った知識のつながり」です。言い換えると「新たに知った知識を追加して、知識のネットワークを広げること」が肝要だということです。
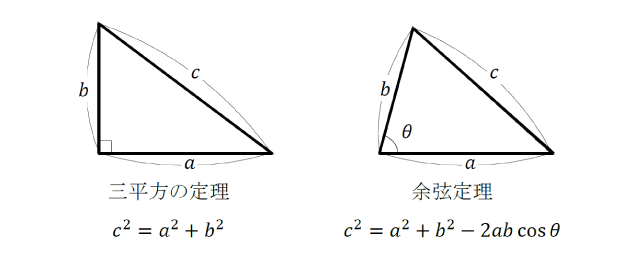
余弦定理を学習する際には、既に学習した三平方の定理との関係性に思いをはせて、
といった共通点や違いを意識して捉えることがポイントなのです。そのように学んでいけば、「余弦定理の式は複雑でよくわからない」、「余弦定理をいつ使えばよいのかわからない」といった悩みに苦しむことは決してありません。
たとえば、「三角比」の単元で余弦定理を学習すると、余弦定理の式を覚えたり使い方を練習したりといったことにとらわれがちです。もちろんそういった演習も大切なのですが、より重要なことは「既に知っている知識と新たに知った知識のつながり」です。言い換えると「新たに知った知識を追加して、知識のネットワークを広げること」が肝要だということです。
余弦定理を学習する際には、既に学習した三平方の定理との関係性に思いをはせて、
- 三平方の定理も余弦定理も、三角形の3辺の長さに関する定理である
- 三平方の定理は直角三角形にしか適用できないが、余弦定理はどのような三角形にも適用することができる
といった共通点や違いを意識して捉えることがポイントなのです。そのように学んでいけば、「余弦定理の式は複雑でよくわからない」、「余弦定理をいつ使えばよいのかわからない」といった悩みに苦しむことは決してありません。