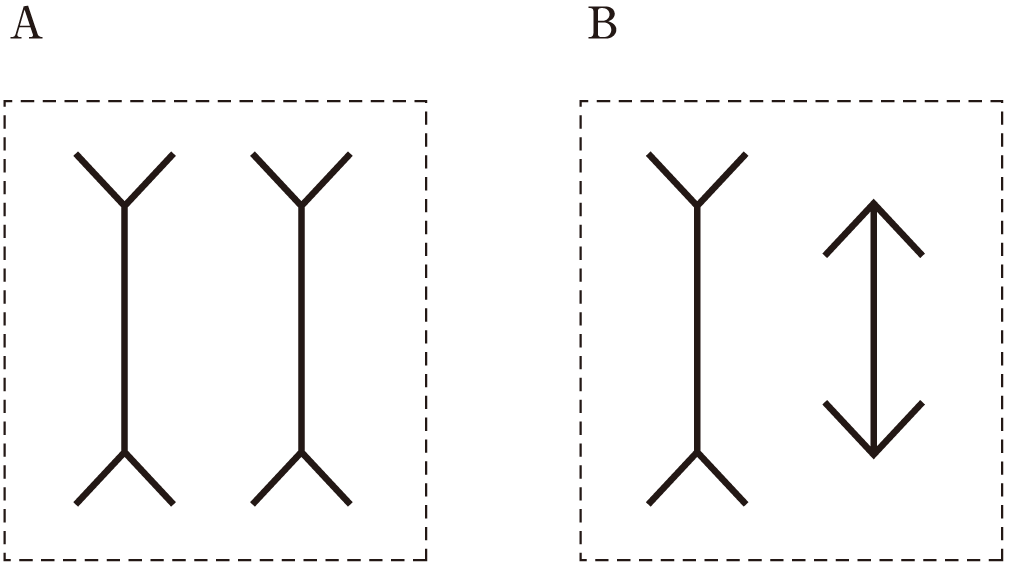
In the following illustration, figure A shows two lines of equal length bounded by arrow-like angles. In figure B, the arrow-like angles are reversed on one of the lines, which changes our perception and creates the illusion of a shorter line. It’s not shorter; measure it and you will find it is equal in length. The lines haven’t changed; your perception of them has.

In figure A, the angles at the end of the lines seem to open up a potentially limited space. Reversing the angle seems to close off and limit the area, which changes your perception of the length of the lines.

A simple reversal of angles dramatically changes what we see in the illustration. The same perceptual changes occur when we reverse our conventional thinking patterns about problems and situations. When Henry Ford went into the automobile business, the conventional thinking was that you had to “bring people to the work.” He reversed this to “bring the work to the people” and accomplished his goal by inventing the assembly line.

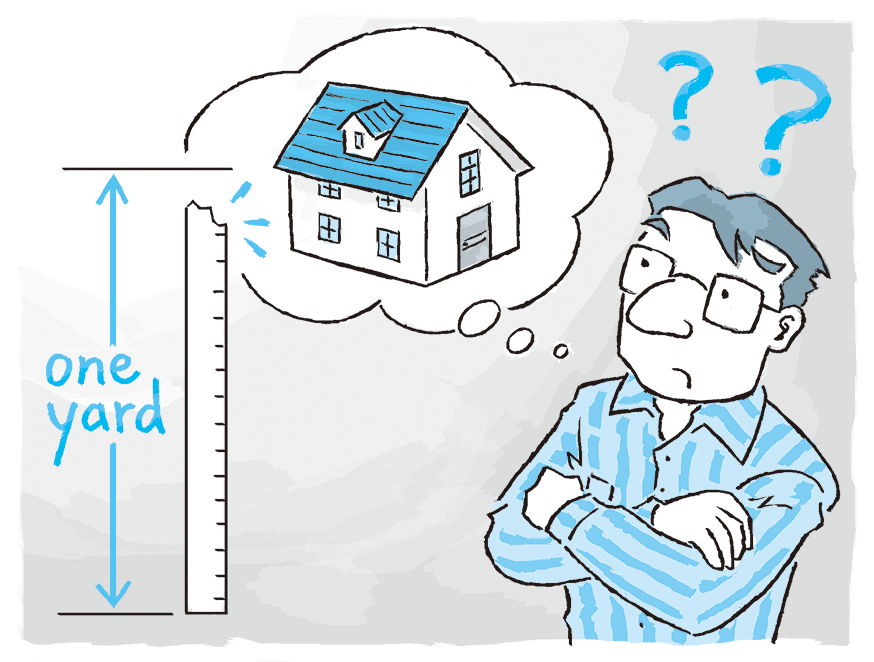
Suppose you built a house using a “yard” stick that was actually an inch short. If you assumed that it was a full yard and used it to measure everything you built, then everything would be wrong, and your ceilings, doors, and windows would be too low. If you had started by questioning the measuring stick, there would have been no problem. It is the same with all problems: If you start with incorrect assumptions, your solutions will be poorly constructed.

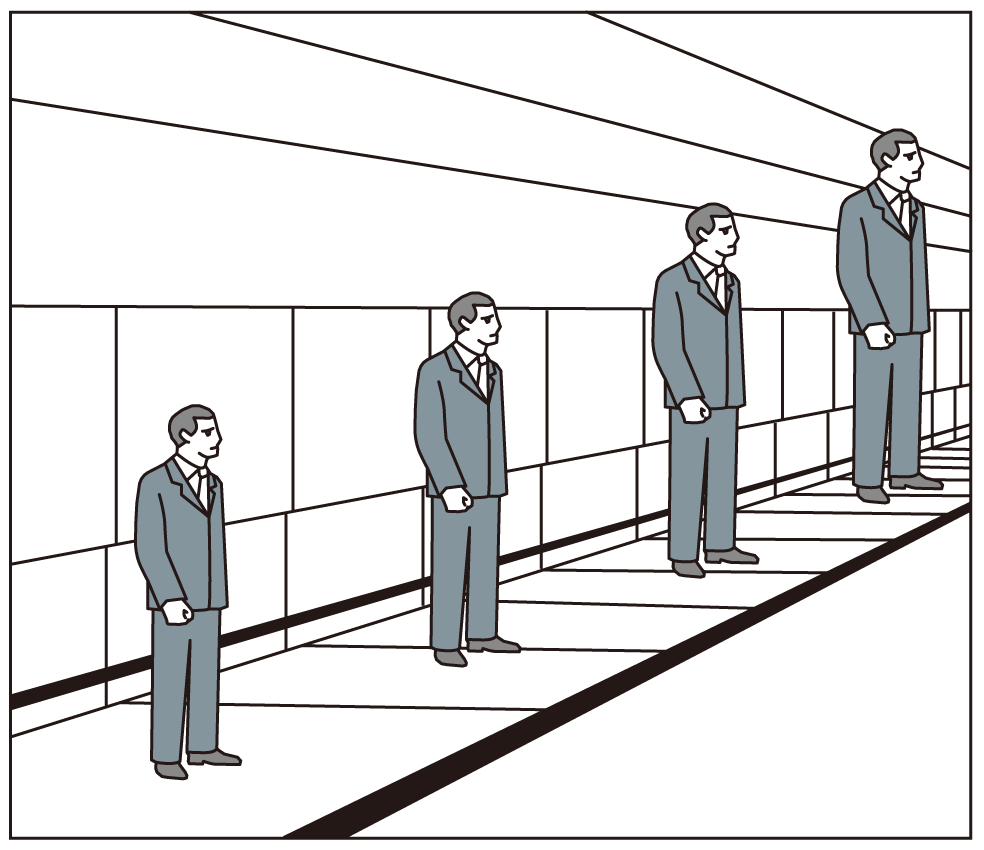
Sometimes assumptions seem so basic, so fundamental, that we never think to challenge them. Consider the following illustration. We assume that the far-away figure, which looks as large as a nearby one, must, in fact, be larger because things are supposed to grow smaller as they move away from us. Yet this assumption doesn’t hold up. Measure the figures with a ruler and you’ll find that they are all the same size.

Assumptions are maintained by the hug of history. Yet, history does not guarantee their validity, nor does it ever reassess their validity. At times, an assumption presents a false face that we mistake for something immutable; a truth that cannot be challenged.

Try to link the nine dots below with no more than three straight lines which will cross through all nine dots, without lifting your pencil.

A surprising number of people will make two assumptions: (1) you must not extend the lines beyond the outside dots, and (2) the lines must pass through the center of each dot. Neither of these “rules” was mentioned above, and once you challenge those assumptions, the problem is easily solved.

Whenever Thomas Edison was about to hire a new employee, he would invite the applicant over for a bowl of soup. If the person salted his soup before tasting it, Edison would not offer him the job. He did not hire people who had too many assumptions built into their everyday life. Edison wanted people who consistently challenged assumptions.

Problems are often salted with assumptions that hinder creativity. Suppose you tell an architect that you want a certain kind of knob on the door between the dining room and kitchen so that it can be easily opened and shut. This illustrates the assumption that the answer to traffic between the two rooms is a door, rather than a redefinition of the space, or of the design, or of how we prepare and eat food. The assumption that a knob is the solution precludes numerous other possibilities.

I put so much emphasis on challenging assumptions to show that any assumption can be challenged. For example, in regard to the illustration of the nine dots, many people assume you cannot link all nine dots with one straight line. You can, and you can do it in several different ways: One way is cut out the dots, line them up in a straight line, and then draw a line through it (below); another is to take a large brush, dip it in paint and swipe it across all the dots.

Obviously, many things have to be taken for granted, and the purpose is not to pretend that one has the time to challenge every assumption, but instead to show nothing is sacrosanct. Once you truly realize this, you are open to all sorts of discoveries. Imagine diving into a lake that everyone assumes is freezing and discovering balmy, warm water. Until you jump, you will never know for sure.