試行調査（プレテスト）の変化を追う_2019.1

2018年11月に、大学入学共通テストの第２回試行調査が実施されました。調査結果の発表はこれからですが、2017年に実施された第1回試行調査からの変更点がありましたので、出題傾向を中心に、Ｚ会の通信教育 高1・高2生向けコース 進路・学習指導担当の山邊圭祐よりお話します。

---

皆さんが最も気にしているのは、記述式問題が導入される数学I・Aと国語でしょうから、この2科目を中心にお伝えします。

2017年の試行調査では、文化祭でのTシャツ販売、観光客の消費動向など、経済に関連した「日常生活や社会問題を数理的に捉える」出題がなされていましたが、今回は学校の階段について、数学的に考察しようとする出題がなされました。

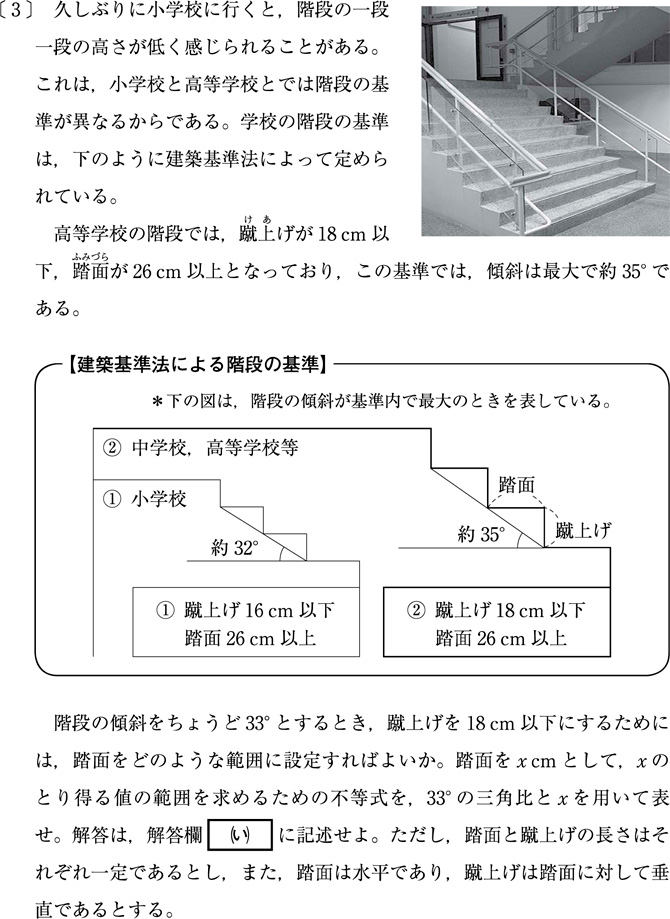
三角比の知識を日常生活に取り入れる出題でしたが、これは2017年５月のモデル問題と同テーマでしたから、受験者にそれほど驚きはなかったはずです。しかし、解答欄「(い)」を埋める記述問題は、少し難しいです。

センター試験では、範囲を求める問題であれば、例えば『「 アイ 」 ＜ ｘ ≦  25』のように、「より大きい」のか「以上」なのかは判断せずとも、値が求まれば正解できる出題となっていました。また、上の例では、「 アイ 」は2桁の正の整数、あるいは「 ア 」に「−（マイナス）」を入れて、1桁の負の整数となることが解答欄の形から明らかなように、解答の形に当てはまる数値が求まらなかったら、間違いであることに容易に気づくことができていました。

今回の試行調査の記述問題は３題と前回調査と変わりませんでしたが、記述量(文字量)は大幅に減少しました。これをもって易しくなったと考えるのは間違いで、受験生が何を記述すべきかをわかりやすくし、採点による評価のブレを最小限に留める改善がなされたと考えるべきです。上述したように、数学記号や日本語を用いて、数学的に正しく表現する必要があることに変わりはありません。そのため、個別試験で数学を必要としない人であっても、自力で正解を記述できる力を養成すること、そのために結果に至るプロセスを確実に理解しておくことが必須となるでしょう。

記述以外の出題では、前回の試行調査よりも問題文が短めになり、読解しやすく改善がなされていました。それでも問題文が長いことに変わりはないため、読解力が求められる試験となることは確実でしょう。

正弦定理を証明する出題です。「太郎さんの証明の構想」では、正しく読解すれば、「カ」に当てはまる正解の文言は、正弦定理の証明方法を知らずとも選択することができます。この前段階で「C=90°」、つまり直角三角形の場合の証明が提示されており、問題文上でそれを利用するように誘導されているためです。つまり問題解決の糸口を、既に解決した問題の解決過程を振り返って考えるという、問題解決のための思考方法が身についているかも問われているわけです。
新テストでは文章の長い問題が多くなる傾向があります。しかし、無駄な文章は1つもなく、問題解決のために必要なヒントが隠されていますので、十分に理解しながら読み進めることも大切です。
このような出題がなされることで、本番も読解量が大幅に増えることが予想されます。例年のセンター試験の問題ページ数に対して、試行調査のページ数は1.5倍程度になっていますので、センター試験の試験時間60分よりも10分増えた70分の試験とはいえ、制限時間内に全ての問題を解ききるためには、相当の訓練が必要だと考えるべきでしょう。

全体的に、センター試験よりも細かい誘導が少なく、発想力等数学の力がしっかり試される試験になりそうなこと、さらに「読解力」と「表現力」が必要となりそうなことに注意して、解答に至る過程を大切にする学習を心がけることが重要です。

前回の試行調査と同様、100分の試験で大問は５題、うち１題が記述式問題、かつ課される小問は３題という構成に変化はありませんでした。また評価も、記述式問題以外で200点、記述式問題の評価は段階評価という点も前回と同様でした。
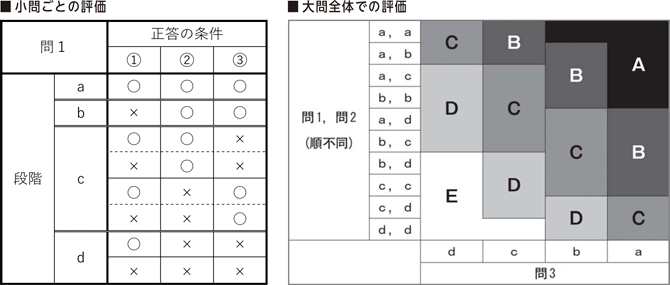
大きな違いは、記述式問題の評価方法でした。今回は「正答の条件」を複数設定し、満たした条件の組合せで、まず小問ごとに「a〜d」の段階評価を付け、さらに3つの小問の評価の組合せによって「A〜E」の5段階に評価される仕組みとなっていました。
「正答の条件」は、「指定文字数を満たしている」「指示された形式に則っている」「解答に必要な内容が含まれている」の3つに大別できます。そのため、最高評価を得るためには、設問の条件を満たすことが必須条件であることがわかります。

以上が「フレーム」の説明になりますが、出題傾向については、2回の試行調査と、その前に発表されたモデル問題から、ある程度の方向性が見えてきましたので、その点をまとめたいと思います。キーワードは「複数の素材文」です。

まず第1問に配置された記述式問題ですが、同テーマの評論文2つを読み、設問に答える形式でした。前回の試行調査では「資料」と「議論」の内容を踏まえて解答する形式でしたが、文章を読解して記述解答を行うという、オーソドックスな出題もなされる可能性があることがわかります。

その代わりに第2問は、評論文に「資料」「表」を加えた素材が提供され、それについて解答する形式でした。「資料」の空欄に当てはまるものを複数解答する形式は目新しいですが、漢字問題が5題出題され、国語表現の問いが出題されるなど、大きくはセンター試験の形式を踏襲した出題でした。

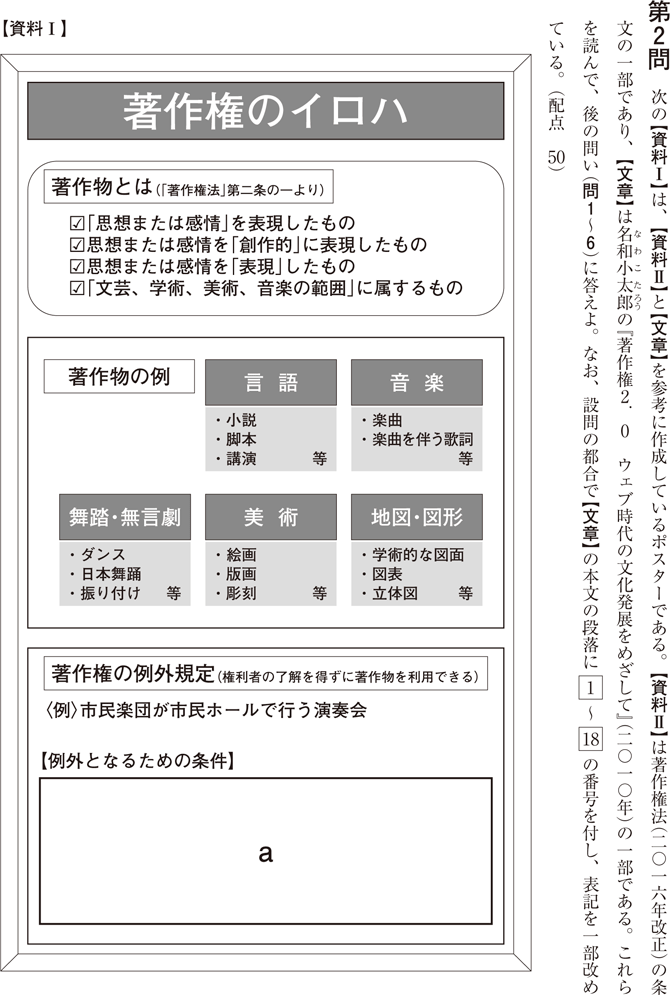
以上から、第1問、第2問では、評論文、あるいは図表などを伴った実用的文章の、論旨の正確な把握を前提として、応用的思考力を問う問題が出題されると考えてよいと思われます。

第3問は、センター試験では小説・随筆が出題される大問に相当しますが、今回の試行調査では、同一作者による「詩」と「エッセイ」を読み、設問に答える形式でした。前回の試行調査は小説という形式ながら、原典となる小説と、それをもとに創作された小説の2つの関連を考えるものでした。これらの出題形式を総合すると、この大問では複数の小説、エッセイ、詩などの文章を提示して、その関連を問う出題がなされるのではないかと推察されます。

現代文が扱われる大問3題では、どんな素材文が出題されるかわからないため、いかなる形式の文章であっても、何種類の文章であっても、資料や図表がいくつ提示されても、そこから読み取るべきことを読み取る読解力・思考力が必要となると考えておきましょう。

第4問の古文は、源氏物語の一節を題材として古文の解釈をした後、古文内の表現に関する生徒と教師の会話をもとに設問に答える形式でした。第5問の漢文は、同様のテーマの現代文と漢文を題材として漢文の解釈をした後、生徒同士の会話文をもとに設問に答える形式でした。2題とも、後半は会話内容をもとに設問に答える形式でしたが、この会話文を「現代文」と考えるならば、前回の試行調査やモデル問題と同様、複数の素材文が提示され、双方の評価を行う形式の設問であることに変わりはありません。
なお、古文・漢文独自の出題については、センター試験の形式、難易度が踏襲されており、基本的に精読ができる力を問われているようです。

以上が皆さんの最も気になる、「記述式問題」が出題される2科目である、数学I・A、国語の分析でした。

他の科目にも着目すべき点がありましたので、列挙しておきます。

センター試験の「筆記」は「筆記(リーディング)」と名前を変え、2回の試行調査ともに大問６題全てが読解問題でしたので、発音・アクセント問題、単独の文法問題が出題されなくなることは、ほぼ確定と考えてよいでしょう。
試験時間に対する英文量、問題量は、センター試験より多くなり、時間的制約はより厳しくなることも確定と考えてよさそうです。
その他、出題される英文がより実用的なもの、図表を絡めたものになる可能性が高く、英文の１文ずつを正確に訳す力よりも、全体の文章の論旨を手早く把握し解答に必要な箇所を素早く検索する能力をより問われる可能性が高いです。そのため、「共通テストのための英語対策」「民間の英語検定試験のための英語対策」「個別試験のための英語対策」と区別するのではなく、総合的に実用的な英語読解能力を高めておくことが重要です。

また、「筆記」「リスニング」の配点がともに100点となったことも大きな変化です。これまでは「筆記」200点、「リスニング」50点でしたから、英語の2技能をバランス良く評価する試験にするという、出題側の意図の表れでしょう。加えて、リスニングでは「アメリカ英語」、「イギリス英語」、「非母語話者の英語」の読み上げがあったことも見逃せません。より実用的な場面での英語聞き取り能力が試されるものとなると理解しましょう。

理科（理科基礎含む）は実験問題や考察問題が増加、地歴・公民は読み取るべき図表、グラフ、史料等が増加しています。また、単に一問一答的に知識で解答できる問題はほぼ出題されていないため、問われていることに対して、問題文で与えられたものを確認しながら知識を組み合わせる力が必要となるでしょう。そのため、全体的に現行のセンター試験よりも難度は上がると考えておいてよさそうです。
ただし、各科目ともに前回の試行調査から出題傾向が若干変わっており、難易度や分量を調整しつつ、ブラッシュアップされる可能性が高いです。


試行調査はこれで終了となる見込みですが、今後の大学入試センターからの発表は見逃せません。まずは、今回の試行調査の結果の発表を待ちましょう。